Standard Deviations

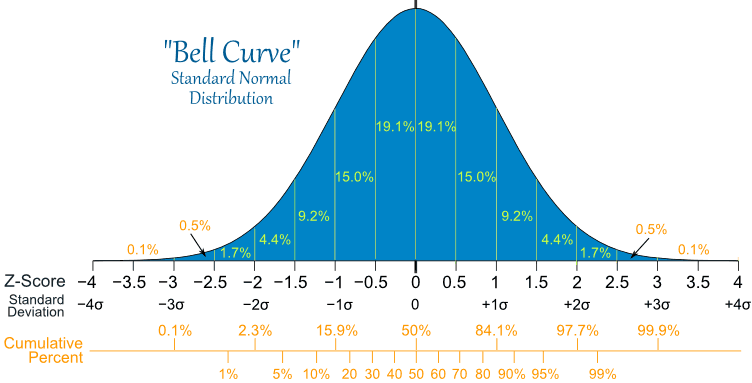
The Standard Deviation is a measure of how spread out numbers are (read that page for details on how to calculate it).

When we calculate the standard deviation we find that (generally):

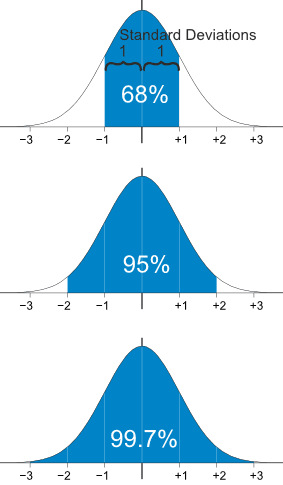68% of values are within 1 standard deviation of the mean 95% of values are within 2 standard deviations of the mean 99.7% of values are within  3 standard deviations of the mean

Example: 95% of students at school are between 1.1m and 1.7m tall.

Assuming this data is normally distributed can you calculate the mean and standard deviation?

The mean is halfway between 1.1m and 1.7m:

Mean = (1.1m + 1.7m) / 2 = 1.4m

95% is 2 standard deviations either side of the mean (a total of 4 standard deviations) so:

1 standard deviation	= (1.7m-1.1m) / 4
	= 0.6m / 4
	= 0.15m

And this is the result:

It is good to know the standard deviation, because we can say that any value is:

• likely to be within 1 standard deviation (68 out of 100 should be)
• very likely to be within 2 standard deviations (95 out of 100 should be)
• almost certainly within 3 standard deviations (997 out of 1000 should be)

Standard Scores

The number of standard deviations from the mean is also called the "Standard Score", "sigma" or "z-score". 

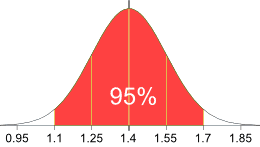
Example: In that same school one of your friends is 1.85m tall

You can see on the bell curve that 1.85m is 3 standard deviations from the mean of 1.4, so: Your friend's height has a "z-score" of 3.0

It is also possible to calculate how many standard deviations 1.85 is from the mean

How far is 1.85 from the mean?

It is 1.85 - 1.4 = 0.45m from the mean

How many standard deviations is that? The standard deviation is 0.15m, so:

0.45m / 0.15m = 3 standard deviations

So to convert a value to a Standard Score ("z-score"):

• first subtract the mean,
• then divide by the Standard Deviation

And doing that is called "Standardizing":

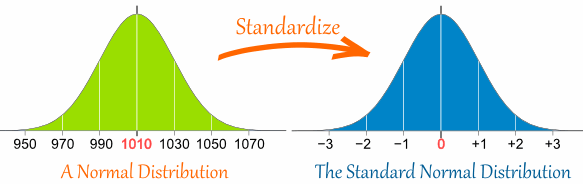
We can take any Normal Distribution and convert it to The Standard Normal Distribution.

Example: Travel Time

A survey of daily travel time had these results (in minutes):

26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32, 28, 34

The Mean is 38.8 minutes, and the Standard Deviation is 11.4 minutes (you can copy and paste the values into the Standard Deviation Calculator if you want).

Convert the values to z-scores ("standard scores").

To convert 26:

first subtract the mean: 26 - 38.8 = -12.8,

then divide by the Standard Deviation: -12.8/11.4 = -1.12

So 26 is -1.12 Standard Deviations from the Mean

Here are the first three conversions

Original Value	Calculation	Standard Score (z-score)
26	(26-38.8) / 11.4 =	-1.12
33	(33-38.8) / 11.4 =	-0.51
65	(65-38.8) / 11.4 =	+2.30
...	...	...

And here they are graphically:

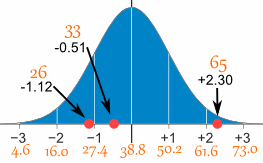
You can calculate the rest of the z-scores yourself!

Here is the formula for z-score that we have been using:

z is the "z-score" (Standard Score) x is the value to be standardized μ is the mean σ is the standard deviation Example: Professor Willoughby is marking a test. Here are the students results (out of 60 points): 20, 15, 26, 32, 18, 28, 35, 14, 26, 22, 17 Most students didn't even get 30 out of 60, and most will fail. The test must have been really hard, so the Prof decides to Standardize all the scores and only fail people 1 standard deviation below the mean. The Mean is 23, and the Standard Deviation is 6.6, and these are the Standard Scores: -0.45, -1.21, 0.45, 1.36, -0.76, 0.76, 1.82, -1.36, 0.45, -0.15, -0.91 Only 2 students will fail (the ones who scored 15 and 14 on the test) It also makes life easier because we only need one table (the Standard Normal Distribution Table), rather than doing calculations individually for each value of mean and standard deviation. Here is the Standard Normal Distribution with percentages for every half of a standard deviation, and cumulative percentages: A Practical Example: Your company packages sugar in 1 kg bags. When you weigh a sample of bags you get these results: 1007g, 1032g, 1002g, 983g, 1004g, ... (a hundred measurements) Mean = 1010g Standard Deviation = 20g Some values are less than 1000g ... can you fix that? The normal distribution of your measurements looks like this: 31% of the bags are less than 1000g, which is cheating the customer! It is a random thing, so we can't stop bags having less than 1000g, but we can try to reduce it a lot. Let's adjust the machine so that 1000g is: at −3 standard deviations: From the big bell curve above we see that 0.1% are less. But maybe that is too small. at −2.5 standard deviations: Below 3 is 0.1% and between 3 and 2.5 standard deviations is 0.5%, together that is 0.1% + 0.5% = 0.6% (a good choice I think) So let us adjust the machine to have 1000g at −2.5 standard deviations from the mean. Now, we can adjust it to: increase the amount of sugar in each bag (which changes the mean), or make it more accurate (which reduces the standard deviation) Let us try both. Adjust the mean amount in each bag The standard deviation is 20g, and we need 2.5 of them: 2.5 × 20g = 50g So the machine should average 1050g, like this: Adjust the accuracy of the machine Or we can keep the same mean (of 1010g), but then we need 2.5 standard deviations to be equal to 10g: 10g / 2.5 = 4g So the standard deviation should be 4g, like this: (We hope the machine is that accurate!) Or perhaps we could have some combination of better accuracy and slightly larger average size, I will leave that up to you! Reference https://www.mathsisfun.com/data/standard-normal-distribution.html