Correlation

When two sets of data are strongly linked together we say they have a High Correlation.

• Correlation is Positive when the values increase together, and
• Correlation is Negative when one value decreases as the other increases

Like this:

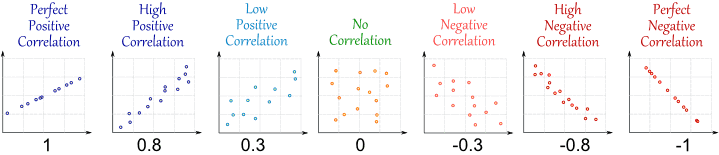
Correlation can have a value:

• 1 is a perfect positive correlation
• 0 is no correlation (the values don't seem linked at all)
• -1 is a perfect negative correlation

The value shows how good the correlation is (not how steep the line is), and if it is positive or negative.

Example: Ice Cream Sales

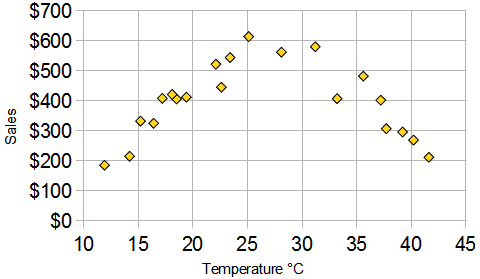
The local ice cream shop keeps track of how much ice cream they sell versus the temperature on that day, here are their figures for the last 12 days:

Ice Cream Sales vs Temperature
Temperature °C	Ice Cream Sales
14.2°	$215
16.4°	$325
11.9°	$185
15.2°	$332
18.5°	$406
22.1°	$522
19.4°	$412
25.1°	$614
23.4°	$544
18.1°	$421
22.6°	$445
17.2°	$408

And here is the same data as a Scatter Plot:

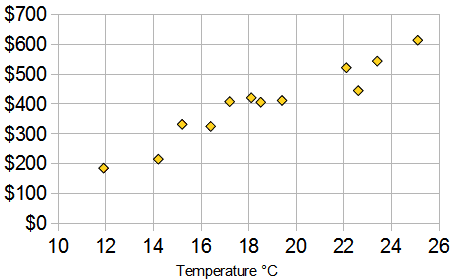
We can easily see that warmer weather leads to more sales, the relationship is good but not perfect.

In fact the correlation is 0.9575 ... see at the end how I calculated.

Correlation Is Not Good at Curves

The correlation calculation only works well for relationships that follow a straight line.

Our Ice Cream Example: there has been a heat wave!

It gets so hot that people aren't going near the shop, and sales start dropping.

Here is the latest graph:

The correlation is now 0: "No Correlation" ... !

The calculated value of correlation is 0 (trust me, I worked it out), which says there is "no correlation".

But we can see the data follows a nice curve that reaches a peak around 25° C. But the correlation calculation is not "smart" enough to see this.

Moral of the story: make a Scatter Plot, and look at it!
You may see more than the correlation value says.

Correlation Is Not Causation

"Correlation Is Not Causation" ... which says that a correlation does not mean that one thing causes the other (there could be other reasons the data has a good correlation).

Example: Sunglasses vs Ice Cream

Our Ice Cream shop finds how many sunglasses were sold by a big store for each day and compares them to their ice cream sales:

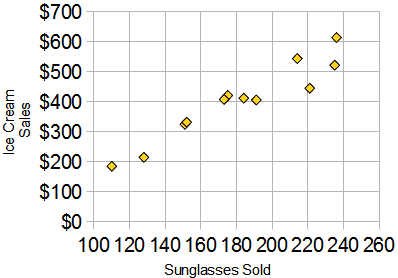
The correlation between Sunglasses and Ice Cream sales is high

Does this mean that sunglasses make people want ice cream?

How To Calculate

How did I calculate the value 0.9575 at the top?

I used "Pearson's Correlation". There is software that can calculate it, such as the CORREL() function in Excel or Open Office Calc ...

... but here is how to calculate it yourself:

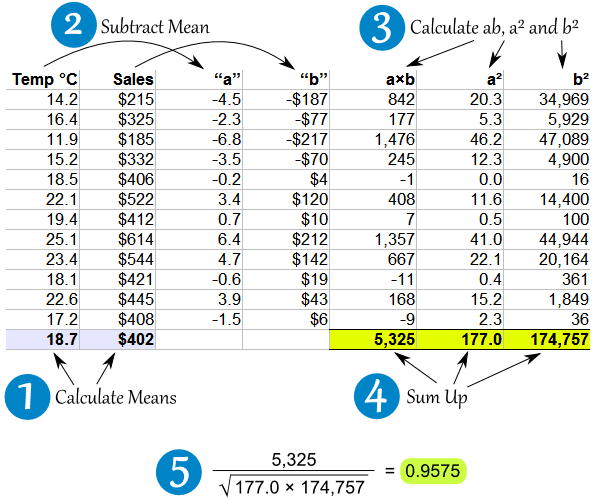
Let us call the two sets of data "x" and "y" (in our case Temperature is x and Ice Cream Sales is y):

• Step 1: Find the mean of x, and the mean of y
• Step 2: Subtract the mean of x from every x value (call them "a"), do the same for y (call them "b")
• Step 3: Calculate: a × b, a² and b² for every value
• Step 4: Sum up a × b, sum up a² and sum up b²
• Step 5: Divide the sum of a × b by the square root of [(sum of a²) × (sum of b²)]

Here is how I calculated the first Ice Cream example (values rounded to 1 or 0 decimal places):

As a formula it is:

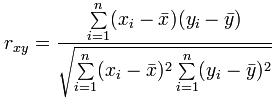
Where:

• Σ is Sigma, the symbol for "sum up"
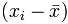•  is each x-value minus the mean of x (called "a" above)
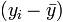•  is each y-value minus the mean of y (called "b" above)

You probably won't have to calculate it like that, but at least you know it is not "magic", but simply a routine set of calculations.

Note for Programmers

You can calculate it in one pass through the data. Just sum up x, y, x², y² and xy (no need for a or b calculations above) then use the formula:

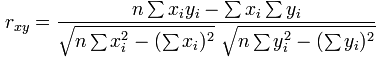
Reference

https://www.mathsisfun.com/data/correlation.html